Update #2

Done

• Read X. Bresson & T. Laurent, An Experimental Study of Neural Networks for Variable Graphs, ICLR 2018
• Read M. Belkin & P. Niyogi, Laplacian Eigenmaps for Dimensionality Reduction and Data Representation, Neural Computation 2003

Experiment 1

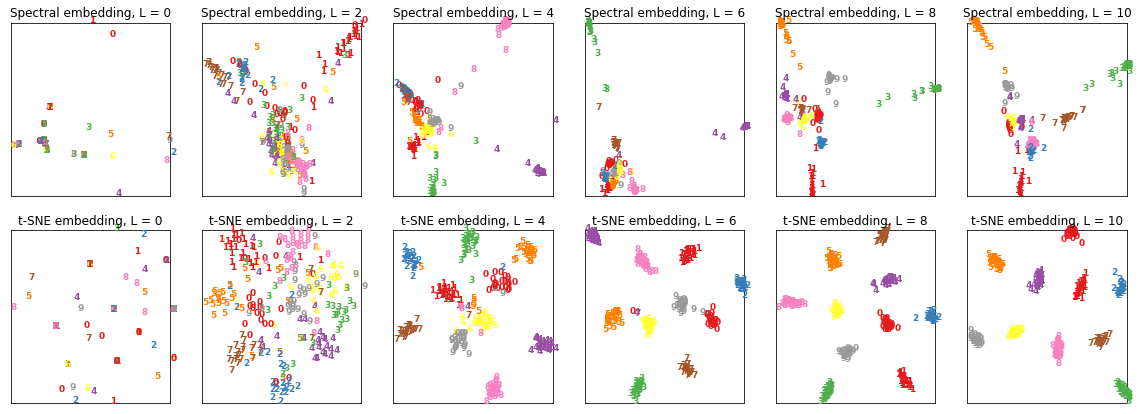
In the following experiment, I consider the graph CNN used for semi-supervised clustering.

The graph CNN is given a graph input consisting of a set of nodes, and passes it through 10 hidden layers, each with an embedding size of 50 dimensions.

Q: Can we visualise the embedding vectors at each hidden layer?

A: Extract the embedding vectors and plot them with non-linear dimensionality reduction!

Here are the results I obtained:

Experiment 2

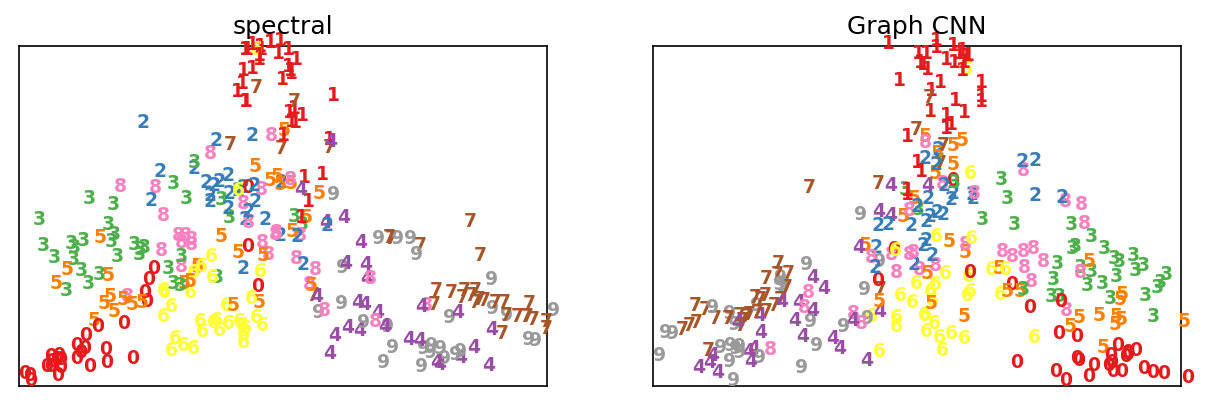
Q: Can we train a graph CNN to perform non-linear dimensionality reduction?

A: Maybe?

Pseudocode for training the net:

# Set up net architecture and parameters
net = GraphConvNet(net_parameters)

for iteration in range(max_iters):
  # Obtain subset of mnist data
  x_train = get_data_subset()

  # Compute affinity matrix
  affinity = affinity_matrix(x_train)

  # Compute training labels from Laplacian eigenmaps
  y_train = spectral_embedding(x_train, affinity)

  # Forward propagation
  y_pred = net.forward(x_train, affinity)

  # Compute L2 loss
  loss = net.loss(y_pred, y_train)

  # Backprop
  loss.backward()

Results after training on MNIST data and spectral embeddings:

Next steps

• Read L.J.P. Maaten & G. Hinton, Visualizing Data using t-SNE, JMLR 2008
• Try different # layers, embedding size, and other hyperparameters
• Find other datasets for non-linear dimensionality reduction?