Note #3: Laplacian Eigenmaps
30 Aug 2018Paper review: M. Belkin & P. Niyogi, Laplacian Eigenmaps for Dimensionality Reduction and Data Representation, Neural Computation 2013
Low effective dimensionality
- Naturally occurring phenomenon often produces intrinsically low-dimensional data lying in a very high-dimensional space
- For example, consider a set of gray-scale images of an object taken by a moving camera
- In such cases, the dimensionality of the data manifold is determined by the degrees of freedom in the data generation process (eg the camera’s movement)
- Even if the manifold is not intrinsic, it might still be practical to visualize the data in lower dimensions
Generalised problem of dimensionality reduction
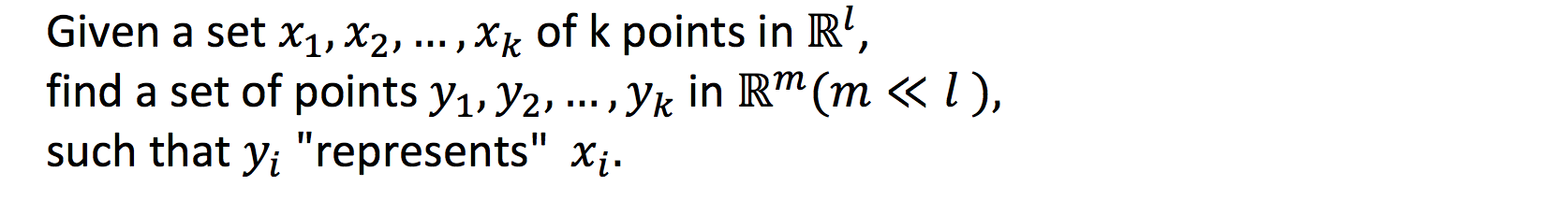
Laplacian Eigenmaps preserve local information optimally
Local information (locality):
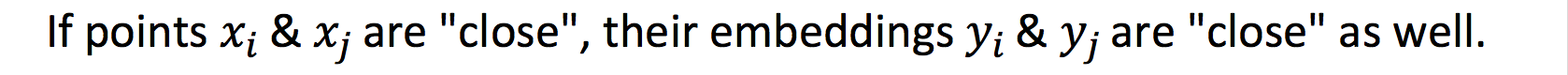
We can encapsulate this property by minimising the following objective function:

Intuitively if two points are close (connected by an edge with large weight), then minimising the objective function will ensure that their embeddings are close.
Expressing our objective function in a quadratic form:
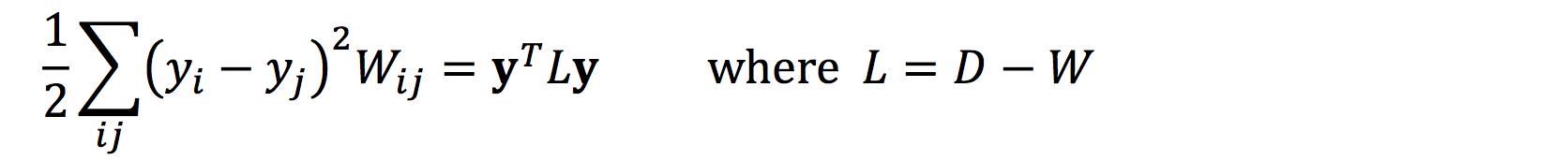
Applying constraints, we can solve the resulting minimization problem with KKT conditions:
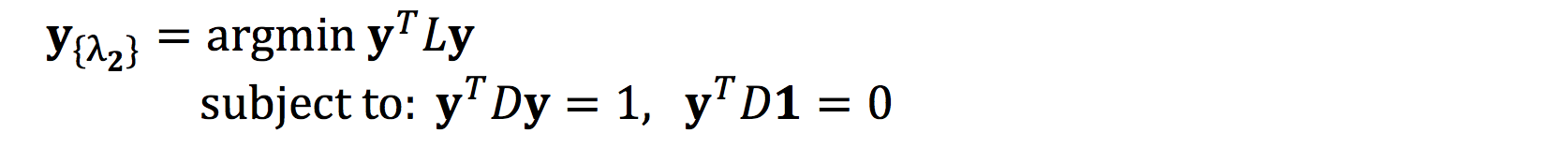
The first constraint removes an arbitrary scaling factor in the embedding.
The second constraint eliminates the trivial solution, ie the eigenvector [1,1, … 1] with eigenvalue 0.
For the m-dimensional embedding problem, the solution is provided by retaining the eigenvectors corresponding to the lowest eigenvalues of the generalised eigenvalue problem:

The embedding is given by the k x m matrix Y, where the ith row provides the embedding coordinates for the ith vertex:

Differences from PCA
Both PCA and Laplacian eigenmaps (LE) are used for dimensionality reduction and involve eigen-decomposition. But the similarity stops there. In fact, they are hugely different approaches to dimensionality reduction.
Operations:
- PCA performs eigen-decomposition on the covariance matrix XTX, derived from the actual data matrix itself.
- LE uses the graph Laplacian, given by some affinity matrix. Hence, LE is more suitable for graph structured data.
Linearity:
- PCA is a linear dimensionality reduction technique. Retained eigenvectors span a subspace that data is then projected onto, thus representing a linear transformation.
- LE is non-linear. Retained eigenvectors directly provide the embedding vectors.
Objective:
- PCA finds the optimal transformations to a subspace with the largest preserved variance.
- LE preserves local information optimally.
Dimensionality reduction and clustering
The local approach to dimensionality reduction imposes a natural clustering of the data.
If we aim to partition objects into two clusters, a common approach is to minimise the normalised cut, which minimises similarity between clusters, while maximising similarity within clusters.
It can be shown that if we relax the binary membership to real values, the solution to the relaxed problem is given by the eigenvector corresponding to the smallest non-zero eigenvalue of the normalised graph Laplacian (aka the Fielder’s vector).
Spectral clustering proceeds by converting the soft membership to a hard clustering with an auxiliary clustering algorithm (eg k-nearest neighbours).
In this sense, dimensionality reduction and clustering are two sides of the same coin. Could we thus measure the quality of a dimensionality reduction method by how well it enhances the cluster properties in the data?