Update #2
10 Sep 2018Done
- Read X. Bresson & T. Laurent, An Experimental Study of Neural Networks for Variable Graphs, ICLR 2018
- Read M. Belkin & P. Niyogi, Laplacian Eigenmaps for Dimensionality Reduction and Data Representation, Neural Computation 2003
Experiment 1
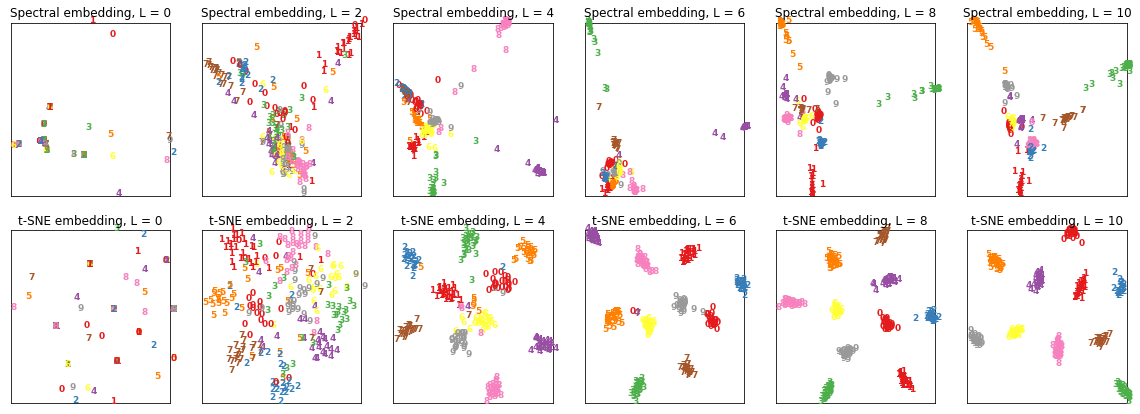
In the following experiment, I consider the graph CNN used for semi-supervised clustering.
The graph CNN is given a graph input consisting of a set of nodes, and passes it through 10 hidden layers, each with an embedding size of 50 dimensions.
Q: Can we visualise the embedding vectors at each hidden layer?
A: Extract the embedding vectors and plot them with non-linear dimensionality reduction!
Here are the results I obtained:
Experiment 2
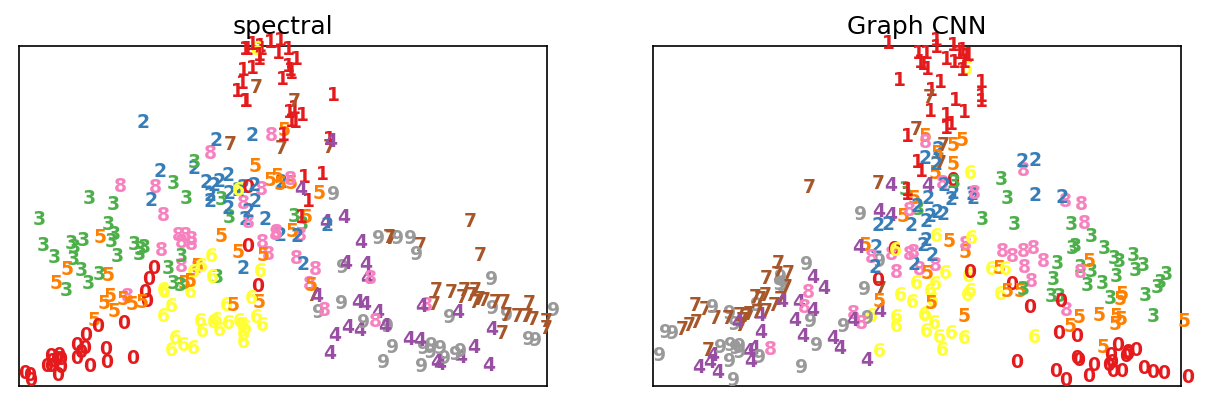
Q: Can we train a graph CNN to perform non-linear dimensionality reduction?
A: Maybe?
Pseudocode for training the net:
# Set up net architecture and parameters
net = GraphConvNet(net_parameters)
for iteration in range(max_iters):
# Obtain subset of mnist data
x_train = get_data_subset()
# Compute affinity matrix
affinity = affinity_matrix(x_train)
# Compute training labels from Laplacian eigenmaps
y_train = spectral_embedding(x_train, affinity)
# Forward propagation
y_pred = net.forward(x_train, affinity)
# Compute L2 loss
loss = net.loss(y_pred, y_train)
# Backprop
loss.backward()
Results after training on MNIST data and spectral embeddings:
Next steps
- Read L.J.P. Maaten & G. Hinton, Visualizing Data using t-SNE, JMLR 2008
- Try different # layers, embedding size, and other hyperparameters
- Find other datasets for non-linear dimensionality reduction?