Update #9

17 Dec 2018

tSNE on graphs

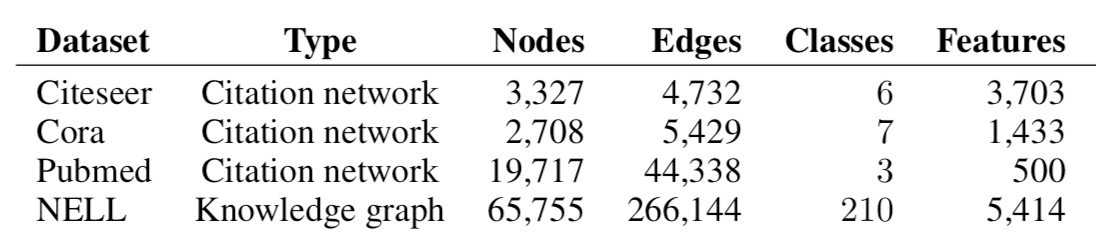
In the following experiments, we will consider datasets consisting of feature nodes in an existing graph structure in the form (X, A) where:

• X is a matrix of feature vectors (n x d)
• A is an adjacency matrix, binary or weighted (n x n)

A note on two losses

To leverage on the graph information, we shall make use of a composite loss, consisting of a tSNE loss and a graph cut loss. This requires two key assumptions about the data:
1. Nodes with similar features should be clustered. (tSNE loss)
2. Nodes with connecting edges should be clustered. (Graph cut loss)

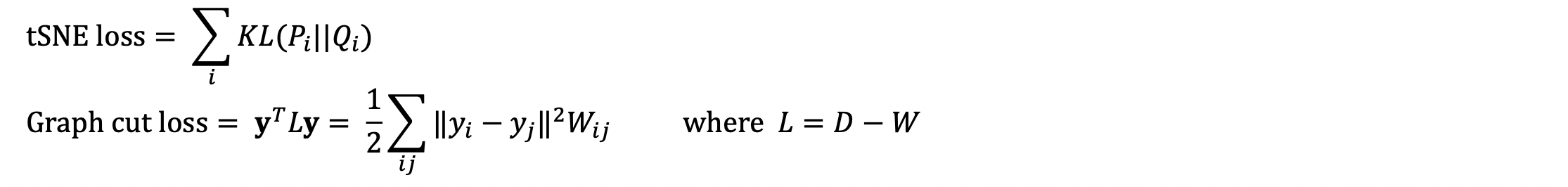
Cora citation network

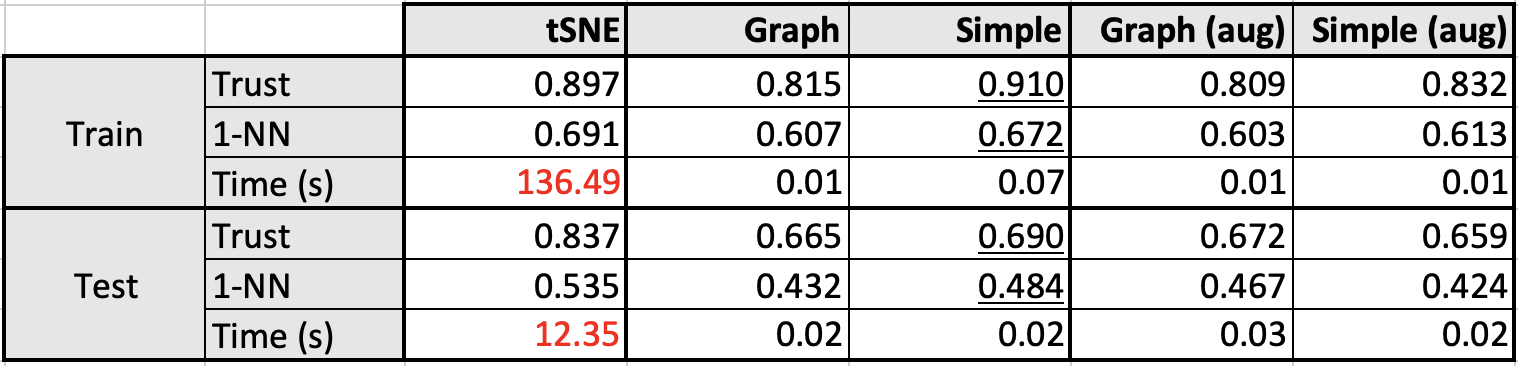
Results

Here, we compare between a graph net and a simple feedforward network.

Preliminary observations

• Minimising the graph cut loss tends to cluster connected nodes together too tightly unless we can enforce a covariance constraint.
• Using cosine distances is very important since the feature vectors are sparse and high dimensional.
• For graph nets, the input size at training time must be similar to the input size at test time.
• Training with randomly sampled subgraphs is important for regularization.

Potential datasets