Update #8

Parametric t-SNE

In Laurens, 2009, the authors propose training a stack of Restricted Boltzmann Machines (RBMs) as a parametric form of t-SNE. In particular, they train a network with 3 hidden layers [500-500-2000] and an output layer of size 2, which represents the predicted 2D embedding.

The training procedure involves performing backprop on the t-SNE loss function. As a refresher, P and Q are the pairwise conditional distributions of data points in the high- and low-dimensional map respectively. With a fixed input, the t-SNE loss function is purely a function of the embedding matrix Y as determined by the network weights.

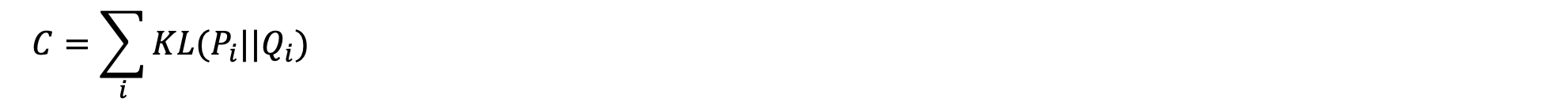
Experiment 1

In the following, two architectures were used: a simple feedforward net (as above) and a graph net. The networks were trained on MNIST data, with a training set of 10,000 samples, using the t-SNE loss above. Both networks were run for 800 epochs.

The trained networks are then used on a test set of 3,000 samples. Below, we compare four visualisations obtained from the following methods: t-SNE, simple net and graph net (both new and old).

Quantitative comparison of the four methods:

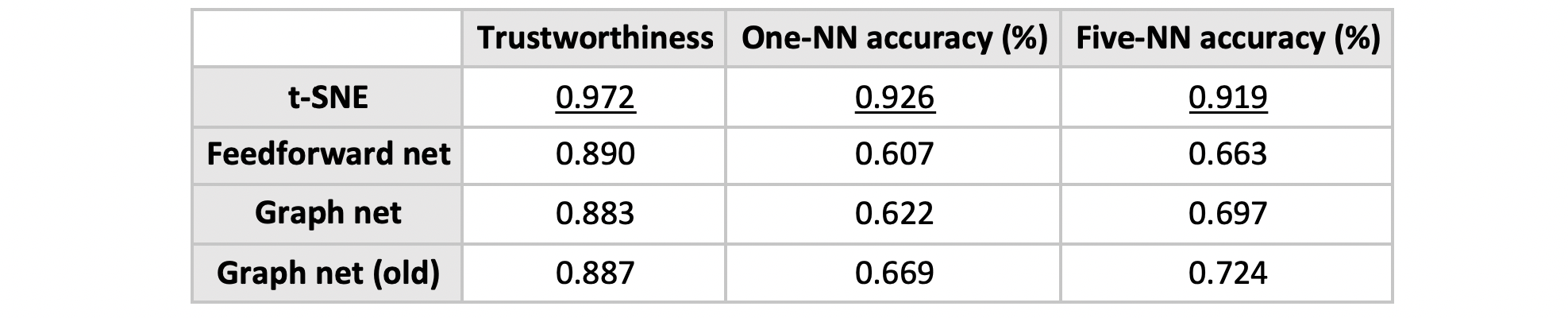
It is possible that the graph net doesn’t work very well because the computed neighbourhood graph is noisy/poorly constructed. Some possible directions include:

• Testing the method on graph structured data like the CORA citation network.
• Finding a way to improve the neighbourhood graph.
• Initializing network weights by supervised training with pre-computed t-SNE samples.