Update #10

27 Dec 2018

Feature clustering vs Graph clustering

Like most dimensionality reduction techniques, tSNE aims to preserve local structure in the high-dimensional data. This means that two points which are similar in high-dimensional space should be close together in the low-dimensional map. Traditionally, the pairwise similarity is given by some distance metric (eg Euclidean or cosine) between two feature vectors. Using tSNE with this distance metric results in clusters having similar features.

On graph-structured data, we can also define a graph-theoretic distance metric based on the shortest path lengths between two nodes. If we now perform tSNE using graph distances, we will obtain clusters belonging to tightly connected graph components. This effect has been observed in graph visualisation techniques like tSNET [Kruiger, 2017] .

By choosing a distance metric, we can either cluster points by feature similarity or graph distances. Based on this, we define two different losses: a feature clustering loss L_X and a graph clustering loss L_G.

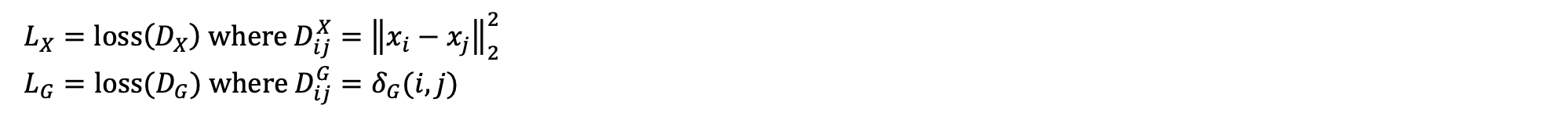
Finally, we can explore the tradeoff between the two losses, by taking a linear combination of the two losses, where the weight of the graph clustering loss is given by a.

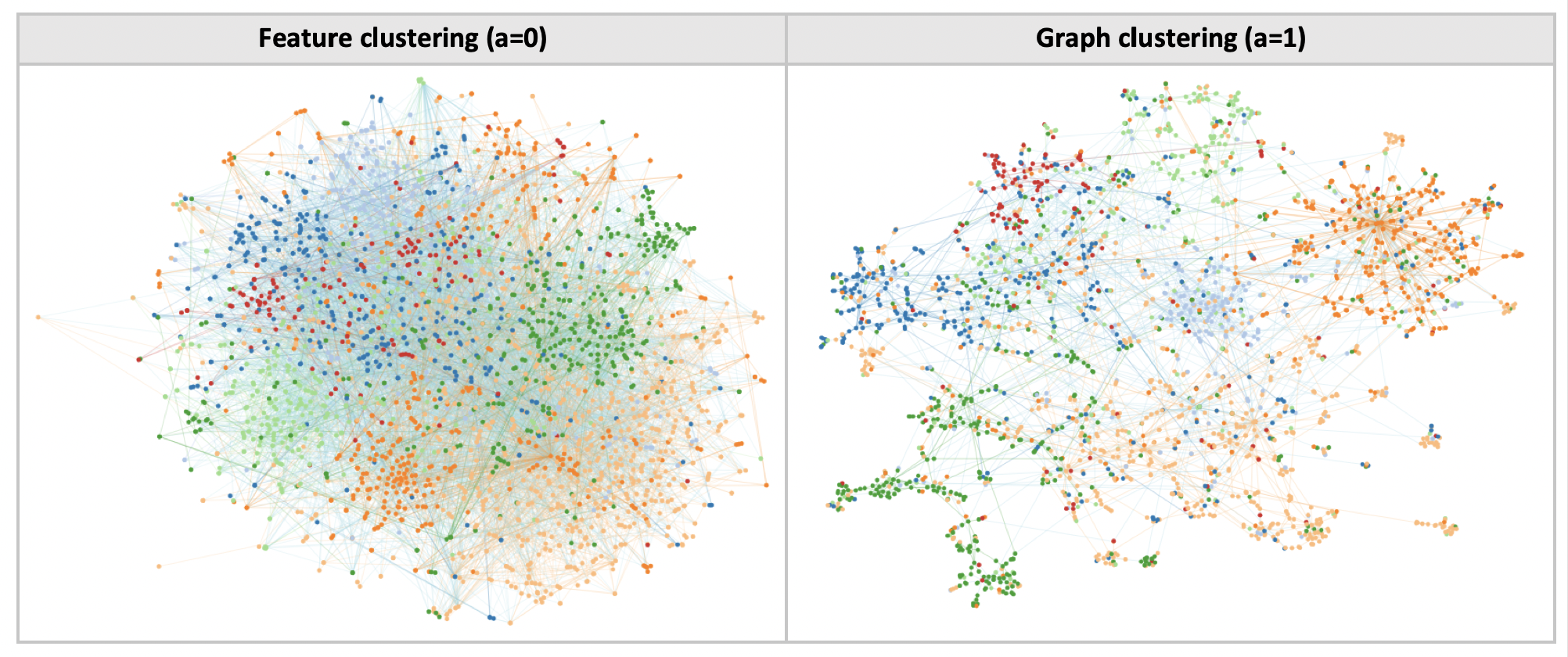
Graph neighborhood preservation metric

Let’s proceed to define graph clustering more precisely. Intuitively, it involves creating a low-dimensional embedding such that the embedding distances between two points are proportional to their graph-theoretic distance. For instance, the nearest neighbours of a given node in the embedding should be its immediate neighbours in the graph.

To capture this intuition, we use a graph neighborhood preservation metric as defined in [Martins, 2015].

Two competing objectives

As seen in [Venna, 2001], the trustworthiness score is a measure of feature neighborhood preservation. A natural question arises: are the two preservation metrics complementary?

Evidently, it is not possible to have it both ways, ie graph and feature neighborhood preservation exist on a tradeoff.

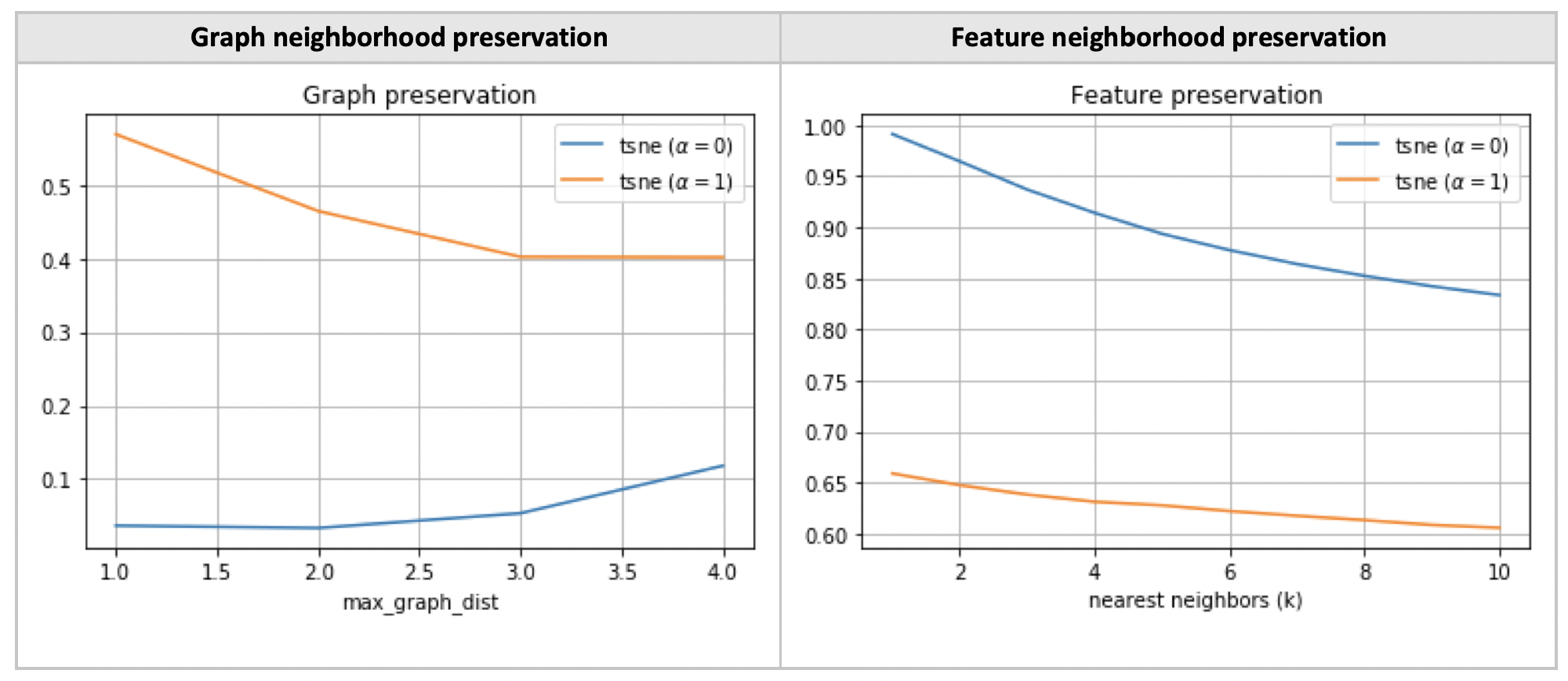
Graph nets are good at preserving graph neighborhoods

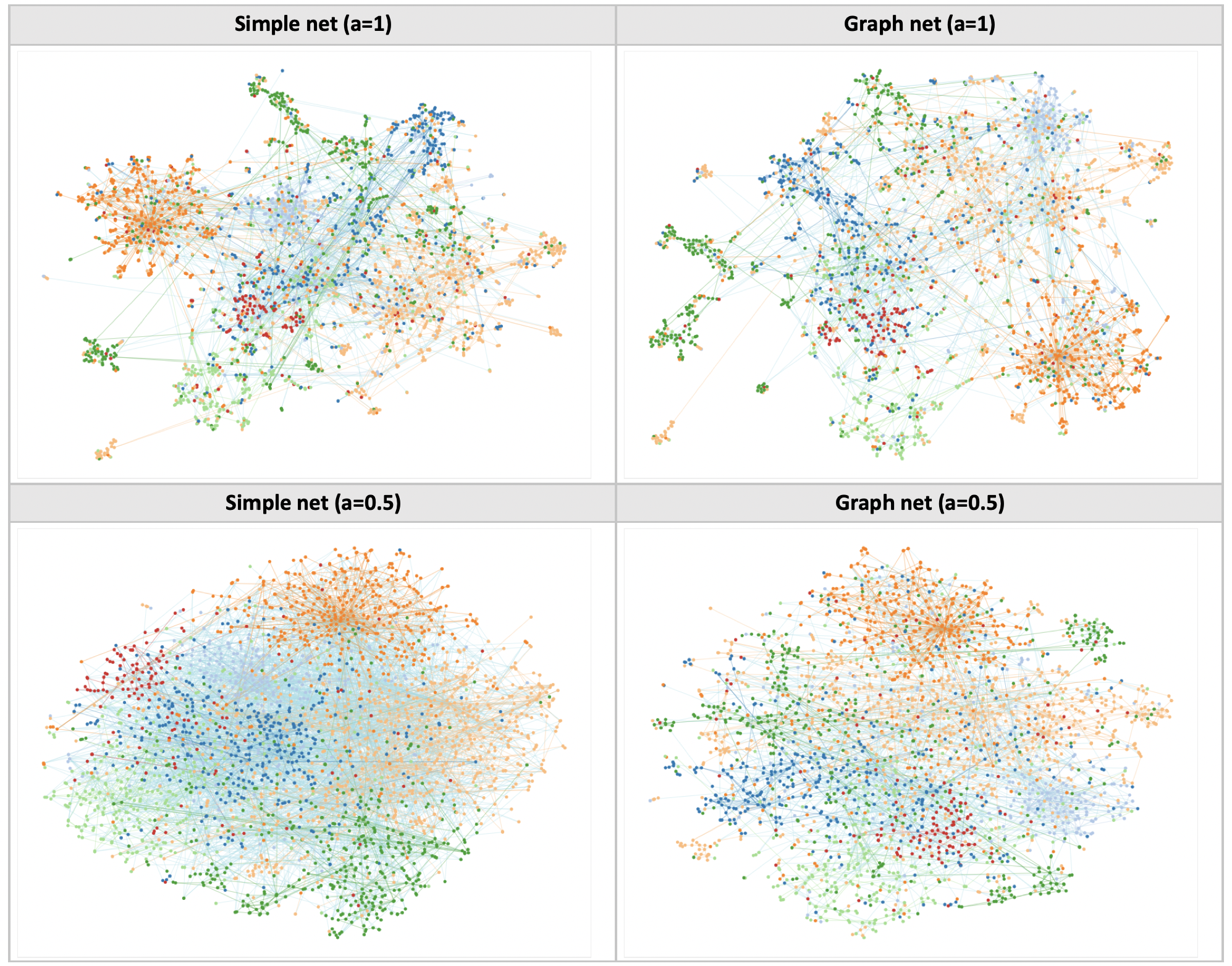
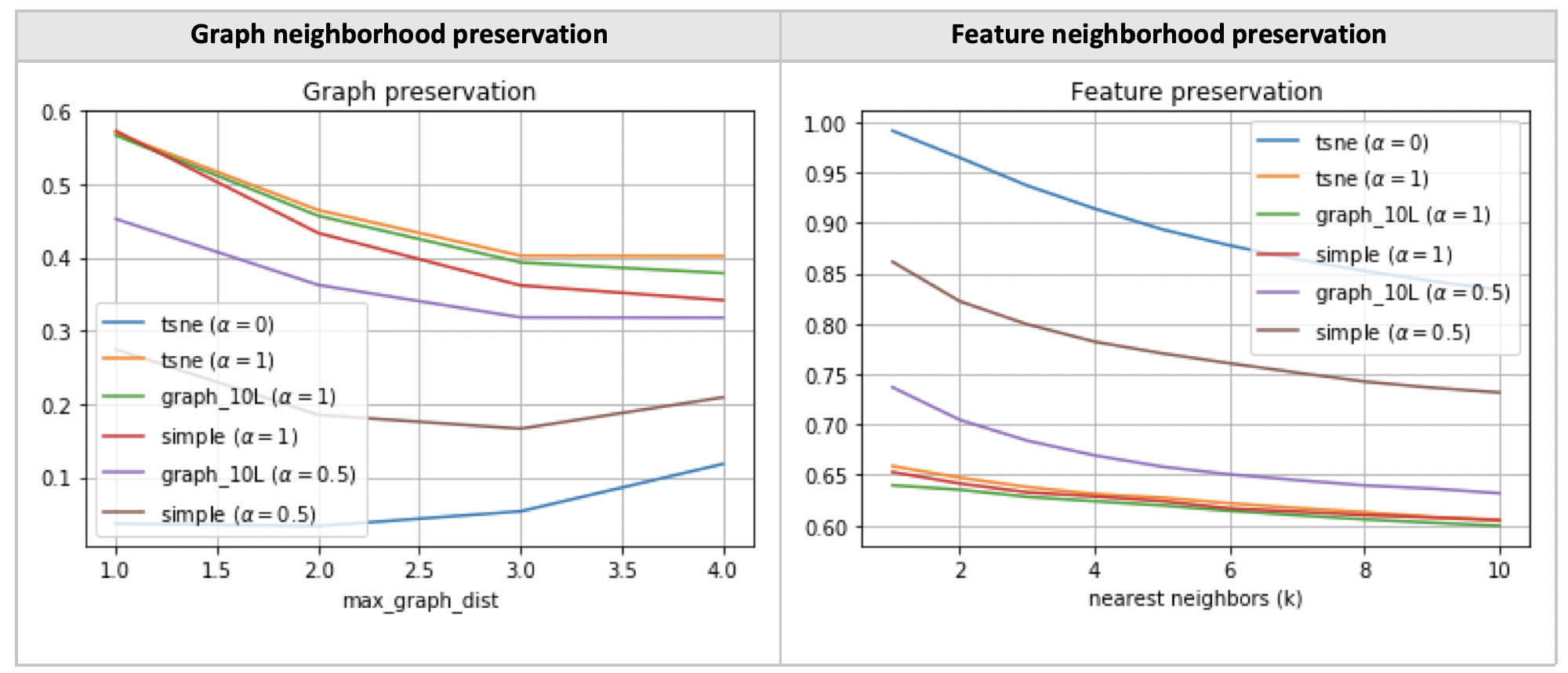
Evidently, the graph nets are better at preserving graph neighborhoods compared to a simple feedforward net. The real question is how can we put this result to good use?

Since we rely on the tSNE loss, standard tSNE can also minimise the same loss by gradient descent. In what way is the graph net more useful than tSNE? Two ideas spring to mind:

• Out-of-sample predictions: Can the trained network be used to predict parts of the graph not included in the training set?
• More scalable training: Can we train the network in batches? Can we somehow stitch the graph together from parts?