Update #3
24 Sep 2018Done
- Set up workflow on Google Cloud Platform: Cloud GPU!
- Lots of experiments (see below)
Experimental set-up
In the following experiments, a reference test set was prepared which consists of 100 separate data sets of sizes in the range [200,500]. Training for spectral used: 6,000 training examples for 100 iterations, in mini-batches of [200,500]
Experiment 1: Evaluation measures
Trustworthiness [Venna, 2001] measures the amount of local structure that is preserved, ranging between [0,1]. A score of 1 roughly indicates that all the nearest neighbours in the high-dimensional space are preserved in the low-dimensional map.
1-NN generalisation error [Maaten, 2009] measures the 10-fold cross-validation error of a one nearest-neighbour classifier trained on the low-dimensional data representations of each test data set.

Experiment 2: Loss function used during training
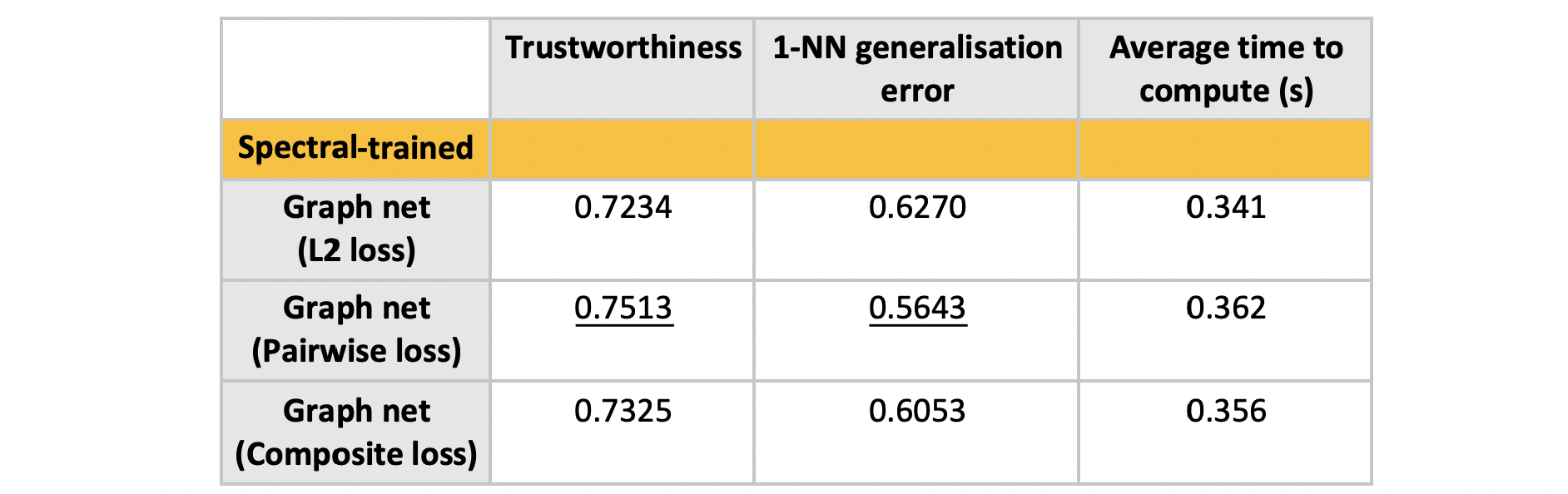
Training on the pairwise loss leads to significant improvements. The L2 loss is not able to reflect the invariance under rotations and reflection when using spectral embeddings.
Experiment 3: Conv net vs Graph net
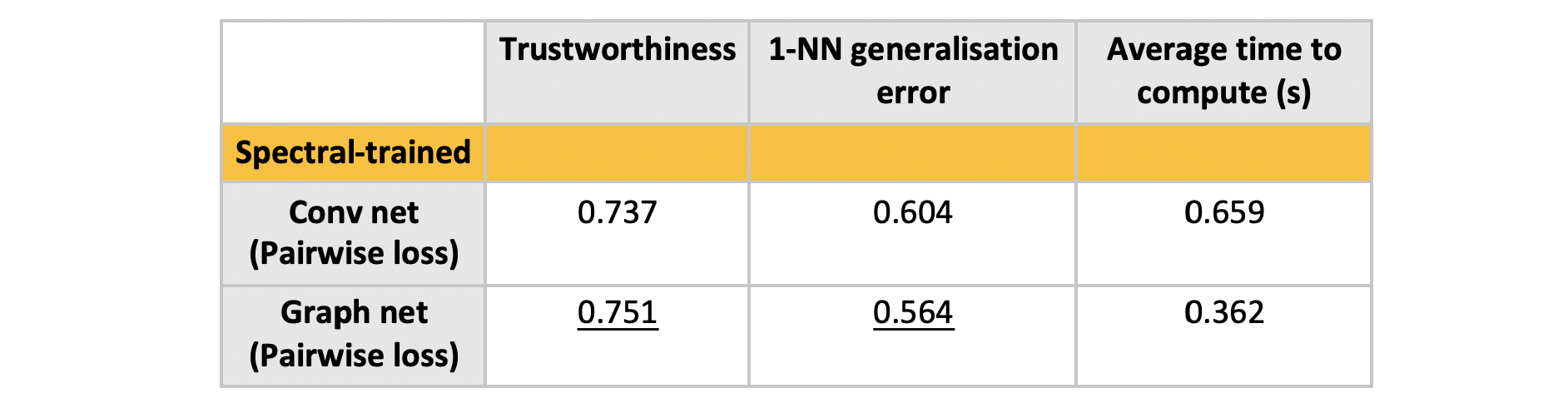
A simple conv net was used with the following architecture:
- Conv 1 (5x5 filters) x50 - ReLU - BatchNorm - MaxPool (3x3, stride 2) -
- Conv 2 (5x5 filters) x50 - ReLU - BatchNorm - MaxPool (3x3, stride 2) -
- Fully connected layer
Comparison of the number of parameters
- Conv net: 68,952
- Graph net: 298,102
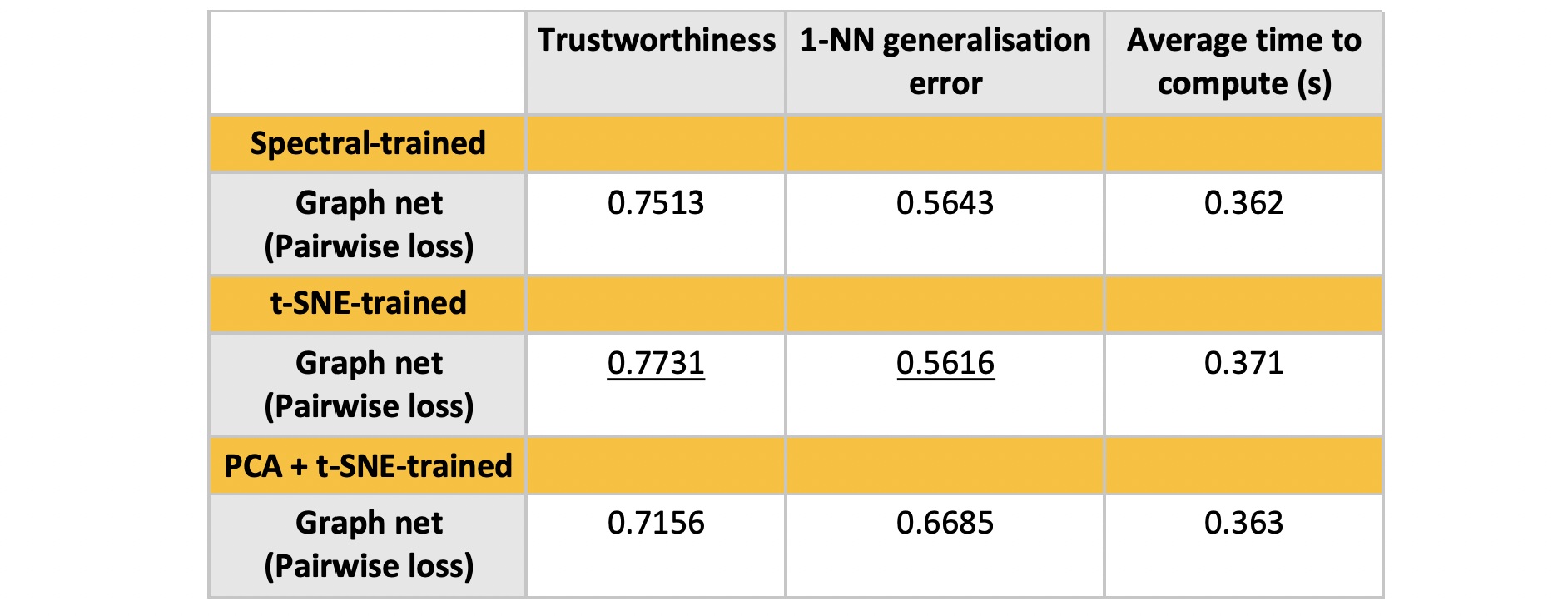
Experiment 4: Training on Spectral vs t-SNE
Training for t-SNE used: 20,000 training examples for 200 iterations, in mini-batches of [200,500]
Experiment 5: Visualising outputs
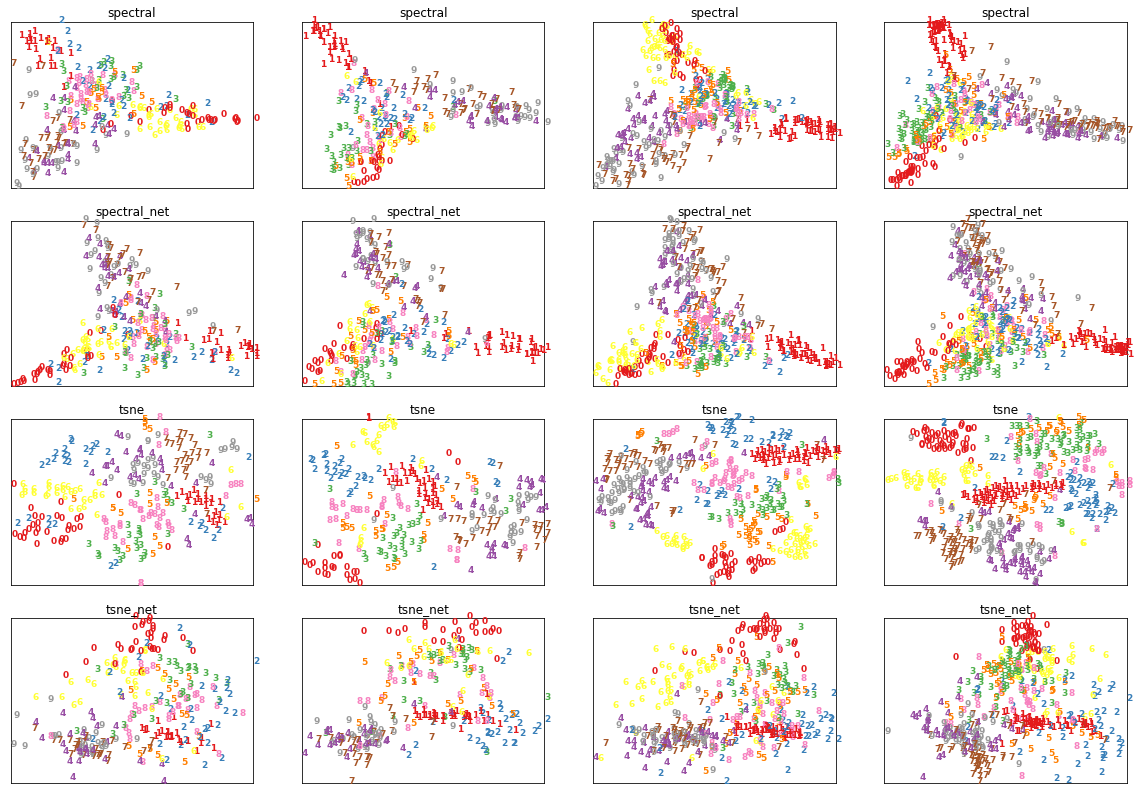
Observations
- The output of the graph net is deterministic; clusters of a certain type always map to the same region in the embedding space.
- The global structure of spectral embeddings is the same in all four cases (subject to rotations and reflections). However, the global structure of t-SNE embeddings varies widely. This is the expected behaviour of t-SNE as the sizes, and the absolute/relative positions of t-SNE clusters may not carry any intrinsic meaning [Waatenberg, 2016].
Experiment 6: Can we learn an inconsistent mapping?
In the following, we consider an oracle embedding which produces a low dimensional mapping by using the knowledge about the image labels.
Deterministic oracle: The first row illustrates an oracle that maps labels into a fixed grid in a consistent manner. For example, all sevens always go into the top left corner. The second row shows that the graph net trained using the pairwise loss is able to learn the clustering of the digits. But because of the pairwise loss, it is also not concerned about learning the grid structure.
Stochastic oracle: The third row illustrates the same oracle, except that the label-grid assignments are randomized. Hence, the oracle does cluster similar points, but in an inconsistent manner. The fourth row shows that the graph net is able to learn some structure, but the resulting clusters are not as distinct as in the previous case. This result is somewhat expected since the task of modelling a stochastic function is considerably harder.
