Note #2: Spectral Analysis on Graphs
19 Aug 2018What does the graph Laplacian represent?
L = D - A
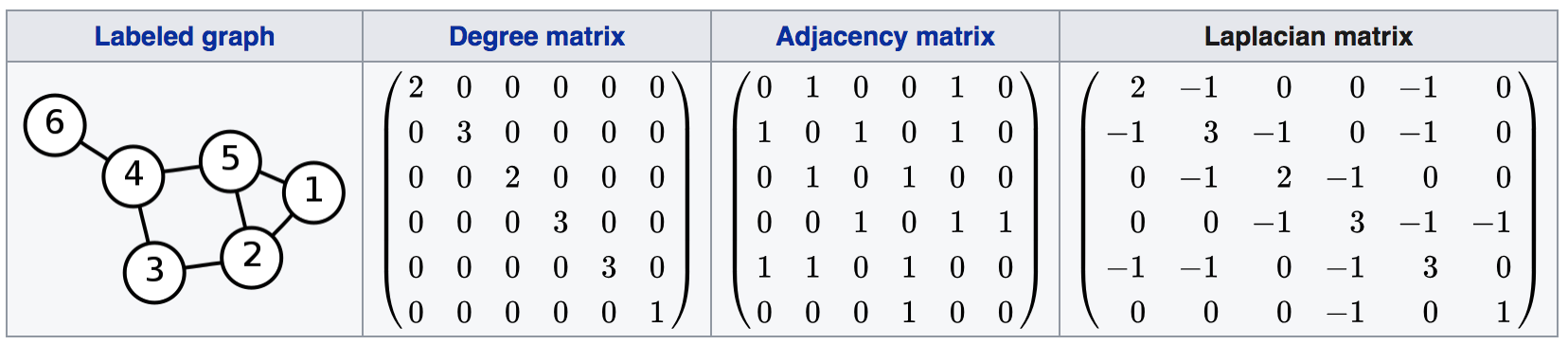
- L is symmetric and positive-semidefinite
- Every row sum and column sum of L is zero.
- L is singular.
- trace(L) = 2m where m is the number of edges of the graph.
- The Laplacian is a local operator since it only considers the immediate neighbors of each node.
Eigenvalues / eigenvectors of L
- Non-negative and real-valued eigenvalues
- N orthogonal eigenvectors
- (1,1,…1) is an eigenvector of L with eigenvalue = 0
- The multiplicity of the eigenvalue 0 is given by the number of connected components in the graph.
- The Fielder value is the second smallest eigenvalue of L and approximates the sparsest cut of a graph.
What does the Fielder value represent?
- The magnitude reflects how well the overall graph is connected.
- The second smallest eigenvalue of L is the solution to an optimisation problem.
Spectral clustering
- Changes the representation of data points using the eigenvectors of the graph Laplacian enhances the cluster properties in the data
- Does not make strong assumptions on the form of the clusters
- Use the normalized graph Laplacian
- Make sure the similarity graph is sparse -> using kNN or epsilon-neighbourhood
- Sensitive to choice of parameters for constructing the neighbourhood graph
Summary of spectral CNN operations
| CNN Operation | In Spectral CNNs |
|---|---|
| Non-linearities | Transform data in the spatial domain |
| Convolution | Filter data in the frequency domain |
| Pooling | Apply graph coarsening, retains a fraction of the graph vertices |
| Conv + stride | Keep only the low-frequency components of the spectrum Subsampling of frequency multipliers + interpolation kernel (cubic splines) |